Skip to main content

Solultion of Triangle - Notes, Concept and All Important Formula

PROPERTIES AND SOLUTIONS OF TRIANGLE

1. SINE FORMULAE :

SINE FORMULAE


In any triangle \(\mathrm{ABC}\)
\(\dfrac{\mathrm{a}}{\sin \mathrm{A}}=\dfrac{\mathrm{b}}{\sin \mathrm{B}}=\dfrac{\mathrm{c}}{\sin \mathrm{C}}=\lambda=\dfrac{\mathrm{abc}}{2 \Delta}=2 \mathrm{R}\)
where \(\mathrm{R}\) is circumradius and \(\Delta\) is area of triangle.


2. COSINE FORMULAE :

(a) \(\mathrm{\cos A=\dfrac{b^{2}+c^{2}-a^{2}}{2 b c}}\) or \(\mathrm{a^{2}=b^{2}+c^{2}-2 b c \cos A}\)
(b) \(\mathrm{\cos B=\dfrac{c^{2}+a^{2}-b^{2}}{2 c a}}\)
(c) \(\mathrm{\cos C=\dfrac{a^{2}+b^{2}-c^{2}}{2 a b}}\)


3. PROJECTION FORMULAE :

(a) \(b \cos C+c \cos B=a\)
(b) \(c \cos A+a \cos C=b\)
(c) \(a \cos B+b \cos A=c\)


4. NAPIER'S ANALOGY (TANGENT RULE) :

(a) \(\tan \left(\dfrac{\mathrm{B}-\mathrm{C}}{2}\right)=\dfrac{\mathrm{b}-\mathrm{c}}{\mathrm{b}+\mathrm{c}} \cot \dfrac{\mathrm{A}}{2}\)

(b) \(\tan \left(\dfrac{\mathrm{C}-\mathrm{A}}{2}\right)=\dfrac{\mathrm{c}-\mathrm{a}}{\mathrm{c}+\mathrm{a}} \cot \dfrac{\mathrm{B}}{2}\)

(c) \(\tan \left(\dfrac{A-B}{2}\right)=\dfrac{a-b}{a+b} \cot \dfrac{C}{2}\)


5. HALF ANGLE FORMULAE :

\(s=\dfrac{a+b+c}{2}=\) semi-perimeter of triangle.

(a) (i) \(\sin \dfrac{A}{2}=\sqrt{\dfrac{(s-b)(s-c)}{b c}}\)
(ii) \(\sin \dfrac{B}{2}=\sqrt{\dfrac{(s-c)(s-a)}{c a}}\)
(iii) \(\sin \dfrac{C}{2}=\sqrt{\dfrac{(s-a)(s-b)}{a b}}\)

(b) (i) \(\cos \dfrac{A}{2}=\sqrt{\dfrac{s(s-a)}{b c}}\)
(ii) \(\cos \dfrac{B}{2}=\sqrt{\dfrac{s(s-b)}{c a}}\)
(iii) \(\cos \dfrac{C}{2}=\sqrt{\dfrac{s(s-c)}{a b}}\)

(c) (i) \(\tan \dfrac{A}{2}=\sqrt{\dfrac{(s-b)(s-c)}{s(s-a)}}=\dfrac{\Delta}{s(s-a)}\)
(ii) \(\tan \dfrac{B}{2}=\sqrt{\dfrac{(s-c)(s-a)}{s(s-b)}}=\dfrac{\Delta}{s(s-b)}\)
(iii) \(\tan \dfrac{C}{2}=\sqrt{\dfrac{(s-a)(s-b)}{s(s-c)}}=\dfrac{\Delta}{s(s-c)}\)

(d) Area of Triangle \(\Delta=\sqrt{s(s-a)(s-b)(s-c)}\)
\(=\dfrac{1}{2} b c \sin A=\dfrac{1}{2} c a \sin B=\dfrac{1}{2} a b \sin C\)
\(=\dfrac{1}{4} \sqrt{2\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2}\right)-a^{4}-b^{4}-c^{4}}\)


6. RADIUS OF THE CIRCUMCIRCLE 'R' :

RADIUS OF THE CIRCUMCIRCLE 'R'
Circumcentre is the point of intersection of perpendicular bisectors of the sides and distance between circumcentre & vertex of triangle is called circumradius 'R'.
\(\mathrm{R}=\dfrac{\mathrm{a}}{2 \sin \mathrm{A}}=\dfrac{\mathrm{b}}{2 \sin \mathrm{B}}=\dfrac{\mathrm{c}}{2 \sin \mathrm{C}}=\dfrac{\mathrm{abc}}{4 \Delta}\).


7. RADIUS OF THE INCIRCLE 'r' :

RADIUS OF THE INCIRCLE 'r'

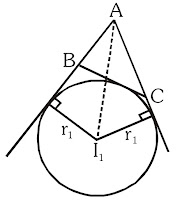
Point of intersection of internal angle bisectors is incentre and perpendicular distance of incentre from any side is called inradius 'r'.


8. RADII OF THE EX-CIRCLES :

RADII OF THE EX-CIRCLES

Point of intersection of two external angle and one internal angle bisectors is excentre and perpendicular distance of excentre from any side is called exradius. If \(r_{1}\) is the radius of escribed circle opposite to angle \(A\) of \(\triangle A B C\) and so on then :

(a) \(\mathrm{r}_{1}=\dfrac{\Delta}{\mathrm{s}-\mathrm{a}}=\mathrm{s} \tan \dfrac{\mathrm{A}}{2}=4 \mathrm{R} \sin \dfrac{\mathrm{A}}{2} \cos \dfrac{\mathrm{B}}{2} \cos \dfrac{\mathrm{C}}{2}\)

(b) \(\mathrm{r}_{2}=\dfrac{\Delta}{\mathrm{s}-\mathrm{b}}=\operatorname{stan} \dfrac{\mathrm{B}}{2}=4 \mathrm{R} \cos \dfrac{\mathrm{A}}{2} \sin \dfrac{\mathrm{B}}{2} \cos \dfrac{\mathrm{C}}{2}\)

(c) \(\mathrm{r}_{3}=\dfrac{\Delta}{\mathrm{s}-\mathrm{c}}=\operatorname{stan} \dfrac{\mathrm{C}}{2}=4 \mathrm{R} \cos \dfrac{\mathrm{A}}{2} \cos \dfrac{\mathrm{B}}{2} \sin \dfrac{\mathrm{C}}{2}\)


9. LENGTH OF ANGLE BISECTOR, MEDIANS & ALTITUDE :

If \(m_{a}, \beta_{a} \) & \(h_{a}\) are the lengths of a median, an angle bisector & altitude from the angle A then,
\(\dfrac{1}{2} \sqrt{b^{2}+c^{2}+2 b c \cos A}=m_{a}=\dfrac{1}{2} \sqrt{2 b^{2}+2 c^{2}-a^{2}}\)
and \(\quad \beta_{a}=\dfrac{2 b c \cos \dfrac{A}{2}}{b+c}, h_{a}=\dfrac{a}{\cot B+\cot C}\)
Note that \(m_{a}^{2}+m_{b}^{2}+m_{c}^{2}=\dfrac{3}{4}\left(a^{2}+b^{2}+c^{2}\right)\)


10. ORTHOCENTRE AND ORTHIC TRIANGLE 

ORTHOCENTRE AND ORTHIC TRIANGLE

(a) Point of intersection of altitudes is orthocentre & the triangle KLM which is formed by joining the feet of the altitudes is called the orthic triangle.

(b) The distances of the orthocentre from the angular points of the \(\Delta \mathrm{ABC}\) are \(2 \mathrm{R} \cos \mathrm{A}, 2 \mathrm{R} \cos \mathrm{B}, \) & \(2 \mathrm{R} \cos \mathrm{C}\)

(c) The distance of orthocentre from sides are \(2 \mathrm{R} \cos \mathrm{B} \cos \mathrm{C}\), \(2 \mathrm{R} \cos C \cos A\) and \(2 \mathrm{R} \cos A \cos B\)

(d) The sides of the orthic triangle are a \(\cos A(=R \sin 2 A)\), \(b \cos B(=R \sin 2 B)\) and \(c \cos C(=R \sin 2 C)\) and its angles are \(\pi-2 A, \pi-2 B\) and \(\pi-2 C\)

(e) Circumradii of the triangles \(\mathrm{PBC}, \mathrm{PCA}, \mathrm{PAB}\) and \(\mathrm{ABC}\) are equal.

(f) Area of orthic triangle \(=2 \Delta \cos A \cos B \cos C\) \(=\dfrac{1}{2} \mathrm{R}^{2} \sin 2 \mathrm{~A} \sin 2 \mathrm{~B} \sin 2 \mathrm{C}\)

(g) Circumradii of orthic triangle \(=\mathrm{R} / 2\)


11. EX-CENTRAL TRIANGLE :

EX-CENTRAL TRIANGLE
(a) The triangle formed by joining the three excentres \(\mathrm{I}_{1}, \mathrm{I}_{2}\) and \(\mathrm{I}_{3}\) of \(\triangle \mathrm{ABC}\) is called the excentral or excentric triangle.

(b) Incentre I of \(\triangle \mathrm{ABC}\) is the orthocentre of the excentral \(\Delta \mathrm{I}_{1} \mathrm{I}_{2} \mathrm{I}_{3}\).

(c) \(\triangle \mathrm{ABC}\) is the orthic triangle of the \(\Delta \mathrm{I}_{1} \mathrm{I}_{2} \mathrm{I}_{3}\).

(d) The sides of the excentral triangle are
\(4 \mathrm{R} \cos \dfrac{\mathrm{A}}{2}, 4 \mathrm{R} \cos \dfrac{\mathrm{B}}{2}\) and \(4 \mathrm{R} \cos \dfrac{\mathrm{C}}{2}\)
and its angles are \(\dfrac{\pi}{2}-\dfrac{A}{2}, \dfrac{\pi}{2}-\dfrac{B}{2}\) and \(\dfrac{\pi}{2}-\dfrac{C}{2}\).

(e) \(\mathrm{II}_{1}=4 \mathrm{R} \sin \dfrac{\mathrm{A}}{2} ; \mathrm{II}_{2}=4 \mathrm{R} \sin \dfrac{\mathrm{B}}{2} ; \mathrm{II}_{3}=4 \mathrm{R} \sin \dfrac{\mathrm{C}}{2}\).


12. THE DISTANCES BETWEEN THE SPECIALPOINTS :

(a) The distance between circumcentre and orthocentre \(=\mathrm{R} \sqrt{1-8 \cos \mathrm{A} \cos \mathrm{B} \cos \mathrm{C}}\)

(b) The distance between circumcentre and incentre \(=\sqrt{\mathrm{R}^{2}-2 \mathrm{Rr}}\)

(c) The distance between incentre and orthocentre \(\mathrm{=\sqrt{2 r^{2}-4 R^{2} \cos A \cos B \cos C}}\)

(d) The distance between circumcentre & excentre is \(=\mathrm{R} \sqrt{1+8 \sin \dfrac{\mathrm{A}}{2} \cos \dfrac{\mathrm{A}}{2} \cos \dfrac{\mathrm{C}}{2}}\)\(=\sqrt{\mathrm{R}^{2}+2 \mathrm{Rr}_1}\) & so on.


13. m-n THEOREM :

m-n THEOREM
(m + n) cot \(\theta\) = m cot \(\alpha\) – n cot \(\beta\)
(m + n) cot \(\theta\) = n cot B – m cot C


14. IMPORTANT POINTS:

(a) (i) If \(a \cos B=b \cos A\), then the triangle is isosceles.
(ii) If \(a \cos A=b \cos B\), then the triangle is isosceles or right angled.

(b) In Right Angle Triangle :

(i) \(a^{2}+b^{2}+c^{2}=8 R^{2}\)
(ii) \(\cos ^{2} A+\cos ^{2} B+\cos ^{2} C=1\)

(c) In equilateral triangle :

(i) \(\mathrm{R}=2 \mathrm{r}\)
(ii) \(r_{1}=r_{2}=r_{3}=\dfrac{3 R}{2}\)
(iii) \(\mathrm{r}: \mathrm{R}: \mathrm{r}_{1}=1: 2: 3\)
(iv) area \(=\dfrac{\sqrt{3} a^{2}}{4}\)
(v) \(\mathrm{R}=\dfrac{\mathrm{a}}{\sqrt{3}}\)
(d) (i) The circumcentre lies (1) inside an acute angled triangle, (2) outside an obtuse angled triangle & (3) at mid point of the hypotenuse of right angled triangle.
(ii) The orthocentre of right angled triangle is the vertex at the right angle.
(iii) The orthocentre, centroid & circumcentre are collinear & centroid divides the line segment joining orthocentre & circumcentre internally in the ratio \(2: 1\), except in case of equilateral triangle. In equilateral triangle all these centres coincide.


15. REGULAR POLYGON :

Consider a 'n' sided regular polygon of side length 'a'.

(a) Radius of incircle of this polygon \(\mathrm{r}=\dfrac{\mathrm{a}}{2} \cot \dfrac{\pi}{\mathrm{n}}\)

(b) Radius of circumcircle of this polygon \(\mathrm{R}=\dfrac{\mathrm{a}}{2} \operatorname{cosec} \dfrac{\pi}{\mathrm{n}}\)

(c) Perimeter & area of regular polygon
Perimeter \(=\mathrm{n} \mathrm{a}=2 \mathrm{nr} \tan \dfrac{\pi}{\mathrm{n}}=2 \mathrm{nR} \sin \dfrac{\pi}{\mathrm{n}}\)
Area \(=\dfrac{1}{2} \mathrm{nR}^{2} \sin \dfrac{2 \pi}{\mathrm{n}}=\mathrm{nr}^{2} \tan \dfrac{\pi}{\mathrm{n}}=\dfrac{1}{4} \mathrm{na}^{2} \cot \dfrac{\pi}{\mathrm{n}}\)


16. CYCLIC QUADRILATERAL :

CYCLIC QUADRILATERAL

(a) Quadrilateral \(\mathrm{ABCD}\) is cyclic if \(\angle \mathrm{A}+\angle \mathrm{C}=\pi\) \(=\angle \mathrm{B}+\angle \mathrm{C}\) (opposite angle are supplementary angles)

(b) Area \(=\sqrt{(s-a)(s-b)(s-c)(s-d)}\), where \(2 s=a+b+c+d\)

(c) \(\cos B=\dfrac{a^{2}+b^{2}-c^{2}-d^{2}}{2(a b+c d)}\) & similarly other angles.

(d) Ptolemy's theorem : If \(A B C D\) is cyclic quadrilateral, then \(\mathrm{AC} \cdot \mathrm{BD}=\mathrm{AB} \cdot \mathrm{CD}+\mathrm{BC} \cdot \mathrm{AD}\)


17. SOLUTION OF TRIANGLE :

Case-I : Three sides are given then to find out three angles use
\(\cos A=\dfrac{b^{2}+c^{2}-a^{2}}{2 b c}, \cos B=\dfrac{c^{2}+a^{2}-b^{2}}{2 a c} \) & \(\cos C=\dfrac{a^{2}+b^{2}-c^{2}}{2 a b}\)

Case-II : Two sides & included angle are given:

Let sides \(a, b \) & angle \(C\) are given then use \(\tan \dfrac{A-B}{2}=\dfrac{a-b}{a+b} \cot \dfrac{C}{2}\) and find value of \(A-B\).....(i)

& \( \dfrac{A+B}{2}=90^{\circ}-\dfrac{C}{2}\)....(ii) \(\quad c=\dfrac{a \sin C}{\sin A}\).....(iii)

Case-III :

SOLUTION OF TRIANGLE

Two sides \(\mathrm{a}, \mathrm{b} \) \(\&\) angle \(\mathrm{A}\) opposite to one of them is given

(a) If \(\mathrm{a}<\mathrm{b} \sin \mathrm{A} \quad\) No triangle exist
(b) If \(a=b \sin A \) & \(A\) is acute, then one triangle exist which is right angled.
(c) \(\mathrm{a}>\mathrm{bsin} \mathrm{A}, \mathrm{a}<\mathrm{b} \) & \(\mathrm{~A}\) is acute, then two triangles exist
(d) \(\mathrm{a}>\mathrm{bsin} \mathrm{A}, \mathrm{a}>\mathrm{b} \) & \(\mathrm{~A}\) is acute, then one triangle exist
(e) \(\mathrm{a}>\mathrm{bsin} \mathrm{A} \) &  \(\mathrm{~A}\) is obtuse, then there is one triangle if \(\mathrm{a}>\mathrm{b}\) & no triangle if \(\mathrm{a}<\mathrm{b}\).

Note : Case-III can be analysed algebraically using Cosine rule as \(\cos A=\dfrac{b^{2}+c^{2}-a^{2}}{2 b c}\), which is quadratic in \(c\).


18. ANGLES OF ELEVATION AND DEPRESSION 

Let OP be a horizontal line in the vertical plane in which an object \(\mathrm{R}\) is given and let OR be joined.

ANGLES OF ELEVATION AND DEPRESSION

In Fig. (a), where the object \(\mathrm{R}\) is above the horizontal line \(\mathrm{OP}\), the angle POR is called the angle of elevation of the object \(\mathrm{R}\) as seen from the point O. In Fig. (b) where the object \(\mathrm{R}\) is below the horizontal line OP, the angle POR is called the angle of depression of the object \(\mathrm{R}\) as seen from the point \(\mathrm{O}\).

Labels:

Comments

Post a Comment

Popular posts from this blog

Indefinite Integration - Notes, Concept and All Important Formula

INDEFINITE INTEGRATION If  f & F are function of \(x\) such that \(F^{\prime}(x)\) \(=f(x)\) then the function \(F\) is called a PRIMITIVE OR ANTIDERIVATIVE OR INTEGRAL of \(\mathrm{f}(\mathrm{x})\) w.r.t. \(\mathrm{x}\) and is written symbolically as \(\displaystyle \int \mathrm{f}(\mathrm{x}) \mathrm{d} \mathrm{x}\) \(=\mathrm{F}(\mathrm{x})+\mathrm{c} \Leftrightarrow \dfrac{\mathrm{d}}{\mathrm{dx}}\{\mathrm{F}(\mathrm{x})+\mathrm{c}\}\) \(=\mathrm{f}(\mathrm{x})\) , where \(\mathrm{c}\) is called the constant of integration. Note : If \(\displaystyle \int f(x) d x\) \(=F(x)+c\) , then \(\displaystyle \int f(a x+b) d x\) \(=\dfrac{F(a x+b)}{a}+c, a \neq 0\) All Chapter Notes, Concept and Important Formula 1. STANDARD RESULTS : (i) \( \displaystyle \int(a x+b)^{n} d x\) \(=\dfrac{(a x+b)^{n+1}}{a(n+1)}+c ; n \neq-1\) (ii) \(\displaystyle \int \dfrac{d x}{a x+b}\) \(=\dfrac{1}{a} \ln|a x+b|+c\) (iii) \(\displaystyle \int e^{\mathrm{ax}+b} \mathrm{dx}\) \(=\dfrac{1}{...
Post a Comment
Read more

Logarithm - Notes, Concept and All Important Formula

LOGARITHM LOGARITHM OF A NUMBER : The logarithm of the number \(\mathrm{N}\) to the base ' \(\mathrm{a}\) ' is the exponent indicating the power to which the base 'a' must be raised to obtain the number \(\mathrm{N}\) . This number is designated as \(\log _{\mathrm{a}} \mathrm{N}\) . (a) \(\log _{a} \mathrm{~N}=\mathrm{x}\) , read as \(\log\) of \(\mathrm{N}\) to the base \(\mathrm{a} \Leftrightarrow \mathrm{a}^{\mathrm{x}}=\mathrm{N}\) . If \(a=10\) then we write \(\log N\) or \(\log _{10} \mathrm{~N}\) and if \(\mathrm{a}=e\) we write \(\ln N\) or \(\log _{e} \mathrm{~N}\) (Natural log) (b) Necessary conditions : \(\mathrm{N}> \,\,0 ; \,\, \mathrm{a}> \,\,0 ; \,\, \mathrm{a} \neq 1\) (c) \(\log _{a} 1=0\) (d) \(\log _{a} a=1\) (e) \(\log _{1 / a} a=-1\) (f) \(\log _{a}(x . y)=\log _{a} x+\log _{a} y ; \,\, x, y> \,\,0\) (g) \(\log _{a}\left(\dfrac{\mathrm{x}}{y}\right)=\log _{\mathrm{a}} \mathrm{x}-\log _{\mathrm{a}} \mathrm{y} ; \,\, \mathrm{...
Post a Comment
Read more

Hyperbola - Notes, Concept and All Important Formula

HYPERBOLA The Hyperbola is a conic whose eccentricity is greater than unity \((e>1) .\) 1. STANDARD EQUATION & DEFINITION(S): Standard equation of the hyperbola is \(\dfrac{\mathbf{x}^{2}}{\mathbf{a}^{2}}-\dfrac{\mathbf{y}^{2}}{\mathbf{b}^{2}}=\mathbf{1},\) where \(b^{2}=a^{2}\left(e^{2}-1\right)\) or \(a^{2} e^{2}=a^{2}+b^{2}\)    i.e.    \(e^{2}=1+\dfrac{b^{2}}{a^{2}}\) \(=1+\left(\dfrac{\text { Conjugate Axis }}{\text { Transverse Axis }}\right)^{2}\) (a) Foci : \(\mathrm{S} \equiv(\mathrm{a} e, 0) \quad \& \quad \mathrm{~S}^{\prime} \equiv(-\mathrm{a} e, 0) .\) (b) Equations of directrices: \(\mathrm{x}=\dfrac{\mathrm{a}}{e}\quad \) & \(\quad \mathrm{x}=-\dfrac{\mathrm{a}}{e}\) (c) Vertices: \(A \equiv(a, 0)\quad \) & \(\quad A^{\prime} \equiv(-a, 0)\) (d) Latus rectum: (i) Equation: \(\mathrm{x}=\pm \mathrm{ae}\) (ii) Length:  \(\begin{aligned} &=\dfrac{2 b^{2}}{a}=\dfrac{(\text { Conjugate Axis })^{2}}{(\text { Transverse Axis ...
Post a Comment
Read more