Skip to main content

Differentiability - Notes, Concept and All Important Formula

DIFFERENTIABILITY

1. INTRODUCTION:

The derivative of a function 'f' is function ; this function is denoted by symbols such as

\(\mathrm{f}^{\prime}(\mathrm{x}), \dfrac{\mathrm{df}}{\mathrm{dx}}, \dfrac{\mathrm{d}}{\mathrm{dx}} \mathrm{f}(\mathrm{x})\) or \(\dfrac{\mathrm{df}(\mathrm{x})}{\mathrm{dx}}\)

The derivative evaluated at a point a, can be written as:

\(\mathrm{f}^{\prime}(\mathrm{a}),\left[\dfrac{\mathrm{df}(\mathrm{x})}{\mathrm{dx}}\right]_{\mathrm{x}=\mathrm{a}}, \mathrm{f}^{\prime}(\mathrm{x})_{\mathrm{x}=\mathrm{a}}\), etc.


2. RIGHT HAND & LEFT HAND DERIVATIVES:

(a) Right hand derivative :

The right hand derivative of \(\mathrm{f}(\mathrm{x})\) at \(\mathrm{x}=\) a denoted by \(\mathrm{f}_{+}^{\prime}(\mathrm{a})\) is defined as :

\(\mathrm{f}_{+}^{\prime}(\mathrm{a})=\displaystyle \lim_{\mathrm{h} \rightarrow 0^{+}} \dfrac{\mathrm{f}(\mathrm{a}+\mathrm{h})-\mathrm{f}(\mathrm{a})}{\mathrm{h}}\), provided the limit exists & is finite.

(b) Left hand derivative :

The left hand derivative of \(f(x)\) at \(x=\) a denoted by \(f^{\prime}(a)\) is defined as \(: f_{-}^{\prime}(a)=\displaystyle \lim_{h \rightarrow 0^{+}} \dfrac{f(a-h)-f(a)}{-h}\), provided the limit exists & is finite.

(c) Derivability of function at a point :

If \(f_{+}^{\prime}(a)=f^{\prime}(a)=\) finite quantity, then \(f(x)\) is said to be derivable or differentiable at \(\mathbf{x}=\mathbf{a}\). In such case \(\mathrm{f}_{+}^{\prime}(\mathrm{a})=\mathrm{f}_{-}^{\prime}(\mathrm{a})=\mathrm{f}^{\prime}(\mathrm{a}) \) & it is called derivative or differential coefficient of \(\mathrm{f}(\mathrm{x})\) at \(\mathrm{x}=\mathrm{a}\).

Note:

(i) All polynomial, trigonometric, inverse trigonometric, logarithmic and exponential function are continuous and differentiable in their domains, except at end points.

(ii) If \(f(x) \) & \(g(x)\) are derivable at \(x=\) a then the functions \(\mathrm{f}(\mathrm{x})+\mathrm{g}(\mathrm{x}), \mathrm{f}(\mathrm{x})-\mathrm{g}(\mathrm{x}), \mathrm{f}(\mathrm{x}) \cdot \mathrm{g}(\mathrm{x})\) will also be derivable at \(\mathrm{x}=\mathrm{a}\) & if \(g(a) \neq 0\) then the function \(f(x) / g(x)\) will also be derivable at \(x=a\).


3. IMPORTANT NOTE :

(a) Let \(\mathrm{f}_{+}^{\prime}(\mathrm{a})=\mathrm{p} \) & \( \mathrm{f}^{\prime}(\mathrm{a})=\mathrm{q}\)

When p & q are finite:

If \(\mathrm{p}\) and \(\mathrm{q}\) are finite (whether equal or not), then \(f\) is continuous at \(\mathrm{x}=\mathrm{a}\) but converse is NOT necessarily true.

Vertical tangent concept

(i) \( \mathrm{p}=\mathrm{q} \Rightarrow \mathrm{f}\) is differentiable at \(\mathrm{x}=\mathrm{a} \Rightarrow \mathrm{f}\) is continuous at \(\mathrm{x}=\mathrm{a}\) \(f^{\prime}(0)=0\) and \(f_{+}^{\prime}(0)=0 \Rightarrow \quad f^{\prime}(0)=0\), here \(\mathrm{x}\) axis is tangent to the curve at \(\mathrm{x}=0\).

(ii) \(\mathrm{p} \neq \mathrm{q} \Rightarrow \mathrm{f}\) is not differentiable at \(\mathrm{x}=\mathrm{a}\), but \(\mathrm{f}\) is still continuous at \(\mathrm{x}=\mathrm{a}\). In this case we have a sudden change in the direction of the graph of the function at \(\mathrm{x}=\mathrm{a}\). This point is called a corner point of the function. At this point there is no tangent to the curve.

When p or q may not be finite :

In this case \(\mathrm{f}\) is not differentiable at \(\mathrm{x}=\mathrm{a}\) and nothing can be concluded about continuity of the function at \(\mathrm{x}=\mathrm{a}\).

Note:

\(\circ\) Corner : If \(\mathrm{f}\) is continuous at \(\mathrm{x}=\) a with \(\mathrm{RHD}\) and \(\mathrm{LHD}\) at \(\mathrm{x}=\mathrm{a}\) both are finite but not equal or exactly one of them is infinite, then the point \(\mathrm{x}=\mathrm{a}\) is called a corner point and at this point function is not differentiable but continuous.


\(\circ\) Cusp : If \(\mathrm{f}\) is continuous at \(\mathrm{x}=\mathrm{a}\) and one of \(\mathrm{RHD}, \mathrm{LHD}\) at \(x=a\), approaches to \(\infty\) and other one approaches to \(-\infty\), then the point \(\mathrm{x}=\mathrm{a}\) is called a cusp point. At cusp point we have a vertical tangent and at this point function is not differentiable but continuous. We can observe that cusp is sharper than corner point.

(b) Geometrical interpretation of differentiability:

(i) If the function \(y=f(x)\) is differentiable at \(x=a\), then a unique tangent can be drawn to the curve \(y=f(x)\) at \(P(a,\), \(\mathrm{f}(\mathrm{a})) \) & \( \mathrm{f}^{\prime}(\mathrm{a})\) represent the slope of the tangent at point \(\mathrm{P}\).

Geometrical interpretation of differentiability

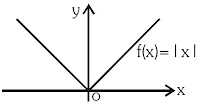
(ii) If LHD and RHD are finite but unequal then it geometrically implies a sharp corner at \(\mathrm{x}=\mathrm{a}\). e.g. \(f(x)=|x|\) is continuous but not differentiable at \(\mathrm{x}=0\).

A sharp corner is seen at \(\mathrm{x}=0\) in the graph of \(f(x)=|x|\).

(c) Vertical tangent : If \(y=f(x)\) is continuous at \(x=\) a and \(\displaystyle \lim _{x \rightarrow a}\left|f^{\prime}(x)\right|\) approaches to \(\infty\), then \(y=f(x)\) has a vertical tangent at \(x=a\). If a function has vertical tangent at \(\mathrm{x}=\mathrm{a}\) then it is non differentiable at \(x=a\).


4. DERIVABILITY OVER AN INTERVAL :

(a) \(\mathrm{f}(\mathrm{x})\) is said to be derivable over an open interval \((\mathrm{a}, \mathrm{b})\) if it is derivable at each & every point of the open interval \((\mathrm{a}, \mathrm{b})\)

(b) \(\mathrm{f}(\mathrm{x})\) is said to be derivable over the closed interval \([\mathrm{a}, \mathrm{b}]\) if :

(i) \(\mathrm{f}(\mathrm{x})\) is derivable in \((\mathrm{a}, \mathrm{b}) \) & 
(ii) for the points a and \(b, f^{\prime}\) \(\left(\right.\) a) &  \( \mathrm{f}^{\prime}\) (b) exist.

Note:

(i) If \(\mathrm{f}(\mathrm{x})\) is differentiable at \(\mathrm{x}=\mathrm{a} \) & \(\mathrm{~g}(\mathrm{x})\) is not differentiable \(\mathrm{at}\) \(x=a\), then the product function \(F(x)=f(x) \cdot g(x)\) can still be differentiable at \(\mathrm{x}=\mathrm{a}\).

(ii) If \(f(x) \) & \(g(x)\) both are not differentiable at \(x=a\) then the product function; \(\mathrm{F}(\mathrm{x})=\mathrm{f}(\mathrm{x}) \cdot \mathrm{g}(\mathrm{x})\) can still be differentiable at \(\mathrm{x}=\mathrm{a}\).

(iii) If \(f(x) \) & \(g(x)\) both are non-derivable at \(x=a\) then the sum function \(\mathrm{F}(\mathrm{x})=\mathrm{f}(\mathrm{x})+\mathrm{g}(\mathrm{x})\) may be a differentiable function.

(iv) If \(\mathrm{f}(\mathrm{x})\) is derivable at \(\mathrm{x}=\mathrm{a} \Rightarrow \mathrm{f}^{\prime}(\mathrm{x})\) is continuous at \(\mathrm{x}=\mathrm{a}\).

(v) Sum or difference of a differentiable and a non-differentiable function is always is non-differentiable.

Labels:

Comments

Post a Comment

Popular posts from this blog

Trigonometry Ratios and Identities - Notes, Concept and All Important Formula

TRIGONOMETRIC RATIOS & IDENTITIES Table Of Contents 1. RELATION BETWEEN SYSTEM OF MEASUREMENT OF ANGLES : \(\dfrac{D}{90}=\dfrac{G}{100}=\dfrac{2 C}{\pi}\) 1 Radian \(=\dfrac{180}{\pi}\) degree \(\approx 57^{\circ} 17^{\prime} 15^{\prime \prime}\) (approximately) 1 degree \(=\dfrac{\pi}{180}\) radian \(\approx 0.0175\) radian All Chapter Notes, Concept and Important Formula 2. BASIC TRIGONOMETRIC IDENTITIES : (a) \(\sin ^{2} \theta+\cos ^{2} \theta=1\) or \(\sin ^{2} \theta=1-\cos ^{2} \theta\) or \(\cos ^{2} \theta=1-\sin ^{2} \theta\) (b) \(\sec ^{2} \theta-\tan ^{2} \theta=1\) or \(\sec ^{2} \theta=1+\tan ^{2} \theta\) or \(\tan ^{2} \theta=\sec ^{2} \theta-1\) (c) If \(\sec \theta+\tan \theta\) \(=\mathrm{k} \Rightarrow \sec \theta-\tan \theta\) \(=\dfrac{1}{\mathrm{k}} \Rightarrow 2 \sec \theta\) \(=\mathrm{k}+\dfrac{1}{\mathrm{k}}\) (d) \(\operatorname{cosec}^{2} \theta-\cot ^{2} \theta=1\) or \(\operatorname{cosec}^{2} \theta=1+\cot ^{2} \th...
Post a Comment
Read more

Inverse Trigonometric function - Notes, Concept and All Important Formula

INVERSE TRIGONOMETRIC FUNCTION 1. DOMAIN, RANGE & GRAPH OFINVERSE TRIGONOMETRIC FUNCTIONS : (a) \(\mathrm{f}^{-1}:[-1,1] \rightarrow[-\pi / 2, \pi / 2]\) , \(\mathrm{f}^{-1}(\mathrm{x})=\sin ^{-1}(\mathrm{x})\) (b) \(\mathrm{f}^{-1}:[-1,1] \rightarrow[0, \pi]\) , \(\mathrm{f}^{-1}(\mathrm{x})=\cos ^{-1} \mathrm{x}\) (c) \(\mathrm{f}^{-1}: \mathrm{R} \rightarrow(-\pi / 2, \pi / 2)\) , \(\mathrm{f}^{-1}(\mathrm{x})=\tan ^{-1} \mathrm{x}\) (d) \(\mathrm{f}^{-1}: \mathrm{R} \rightarrow(0, \pi)\) \(\mathrm{f}^{-1}(\mathrm{x})=\cot ^{-1} \mathrm{x}\) (e) \(\mathrm{f}^{-1}:(-\infty,-1] \cup[1, \infty)\) \(\rightarrow[0, \pi / 2) \cup(\pi / 2, \pi]\) , \(\mathrm{f}^{-1}(\mathrm{x})=\sec ^{-1} \mathrm{x}\) (f) \(\mathrm{f}^{-1}:(-\infty,-1] \cup[1, \infty)\) \(\rightarrow[-\pi / 2,0) \cup(0, \pi / 2]\) \(\mathrm{f}^{-1}(\mathrm{x})=\operatorname{cosec}^{-1} \mathrm{x}\) All Chapter Notes, Concept and Important Formula 2. PROPERTIES OF INVERSE CIRCULAR FUNCTIONS: Property-1 : (i) \(y=\sin ...
Post a Comment
Read more

3d Coordinate Geometry - Notes, Concept and All Important Formula

3D-COORDINATE GEOMETRY 1. DISTANCE FORMULA: The distance between two points \(A \left( x _{1}, y _{1}, z _{1}\right)\) and \(B \left( x _{2}, y _{2}, z _{2}\right)\) is given by \(A B=\sqrt{\left[\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}\right]}\) All Chapter Notes, Concept and Important Formula 2. SECTION FORMULAE : Let \(P \left( x _{1}, y _{1}, z _{1}\right)\) and \(Q \left( x _{2}, y _{2}, z _{2}\right)\) be two points and let \(R ( x , y , z )\) divide \(PQ\) in the ratio \(m _{1}: m _{2}\) . Then \(R\) is \((x, y, z)=\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}, \frac{m_{1} z_{2}+m_{2} z_{1}}{m_{1}+m_{2}}\right)\) If \(\left( m _{1} / m _{2}\right)\) is positive, \(R\) divides \(PQ\) internally and if \(\left( m _{1} / m _{2}\right)\) is negative, then externally. Mid point of \(PQ\) is given by \(\left(\frac{ x _{1}+ x _{2}}{2}, \frac{ y _{1}+ y _{2}}{2}, \frac{ z _{1}+ z ...
Post a Comment
Read more