Skip to main content

Function (Mathematics)- Notes, Concept and All Important Formula

FUNCTION

1. DEFINITION :

If to every value (considered as real unless other-wise stated) of a variable \(\mathrm{x}\), which belongs to a set \(\mathrm{A}\), there corresponds one and only one finite value of the quantity \(y\) which belong to set \(B\), then \(y\) is said to be a function of \(x\) and written as \(f: A \rightarrow B, y=f(x), x\) is called argument or independent variable and \(y\) is called dependent variable.

Pictorially: \( \underset{\text { input }}{\stackrel{\mathrm{x}}{\longrightarrow}}\boxed{\mathrm{f}}\,\,  \underset{\text { output }}{\stackrel{\mathrm{f(x)=y}}{\longrightarrow}}\)

\(y\) is called the image of \(x\) and \(x\) is the pre-image of \(y\), under mapping \(\mathrm{f}\). 
Every function \(\mathrm{f}: \mathrm{A} \rightarrow \mathrm{B}\) satisfies the following conditions.
(i) \(f \subset A \times B\)
(ii) \(\forall \,\,  a \in A \,\, \exists\,\, b \in B\) such that \((a, b) \in f\) and
(iii) If \((a, b) \in f \) & \((a, c) \in f \Rightarrow b=c\)


2. DOMAIN, CO-DOMAIN & RANGE OF A FUNCTION:

Let \(f: A \rightarrow B\), then the set \(A\) is known as the domain of 'f' & the set \(B\) is known as co-domain of 'f'. The set of all f images of elements of \(A\) is known as the range of ' \(f^{\prime}\). Thus

  • Domain of \(\mathrm{f}=\{\mathrm{x} \mid \mathrm{x} \in \mathrm{A},(\mathrm{x}, \mathrm{f}(\mathrm{x})) \in \mathrm{f}\}\)
  • Range of \(\mathrm{f}=\{\mathrm{f}(\mathrm{x}) \mid \mathrm{x} \in \mathrm{A}, \mathrm{f}(\mathrm{x}) \in \mathrm{B}\}\)
  • Range is a subset of co-domain.


3. IMPORTANT TYPES OF FUNCTION :

(a) Polynomial function:

If a function 'f' is called by \(f(x)\)\(=a_{0} x^{n}\)\(+a_{1} x^{n-1}\)\(+a_{2} x^{n-2}+\ldots \)\(\ldots\)\(+a_{n-1} x\)\(+a_{n}\) where \(n\) is a non negative integer and \(a_{0}, a_{1}, a_{2}, \ldots . a_{n}\) are real numbers and \(\mathrm{a}_{0} \neq 0\), then \(\mathrm{f}\) is called a polynomial function of degree \(\mathrm{n}\).

Note:
(i) A polynomial of degree one with no constant term is called an odd linear function. i.e. \(\mathrm{f}(\mathrm{x})=\mathrm{ax}, \mathrm{a} \neq 0.\)
(ii) There are four polynomial functions, satisfying the relation ; \(\mathrm{f}(\mathrm{x}) \cdot \mathrm{f}(1 / \mathrm{x})=\mathrm{f}(\mathrm{x})+\mathrm{f}(1 / \mathrm{x})\). They are:

  • \(\mathrm{f}(\mathrm{x})=\mathrm{x}^{\mathrm{n}}+1, \mathrm{n} \in \mathbb{N}\)
  • \(\mathrm{f}(\mathrm{x})=1-\mathrm{x}^{\mathrm{n}}, \mathrm{n} \in \mathbb{N}\)
  • \(\mathrm{f}(\mathrm{x})=0\)
  • \(f(x)=2\)
(iii) Domain of a polynomial function is \(\mathrm{R}\).
(iv) Range of odd degree polynomial is \(\mathrm{R}\) whereas range of an even degree polynomial is never \(\mathrm{R}\).

(b) Algebraic function :

A function 'f' is called an algebraic function if it can be constructed using algebraic operations (such as addition, subtraction, multiplication, division, and taking radicals) starting with polynomials.

(c) Rational function :

A rational function is a function of the form \(y=f(x)=\frac{g(x)}{h(x)}\), where \(g(x) \) & \( h(x)\) are polynomials & \( h(x) \neq 0\)
Domain : \(\mathrm{R}-\{\mathrm{x} \mid \mathrm{h}(\mathrm{x})=0\}\)
Any rational function is automatically an algebraic function.

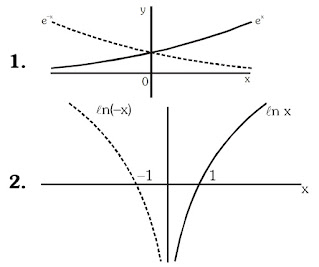
(d) Exponential and Logarithmic Function:

A function \(\mathrm{f}(\mathrm{x})=\mathrm{a}^{\mathrm{x}}(\mathrm{a}>0), \mathrm{a} \neq 1, \mathrm{x} \in \mathrm{R}\) is called an exponential function. The inverse of the exponential function is called the logarithmic function, i.e. \(g(x)=\log _{a} x\)

Note that \(\mathrm{f}(\mathrm{x}) \) & \( \mathrm{~g}(\mathrm{x})\) are inverse of each other \(\&\) their graphs are as shown. (Functions are mirror image of each other about the line \(y=x)\)

Domain of \(a^{x}\) is \(R \quad\) Range \(R^{+}\) 
Domain of \(\log _{a} x\) is \(R^{+} \quad\) Range \(R\)
Graph of Exponential and Logarithmic Function graph

(e) Absolute value function:

Graph of Absolute value function:

It is defined as : \(y=|x|\)

\(=\left\{\begin{array}{rll}\mathrm{x} & \text { if } & \mathrm{x} \geq 0 \\ -\mathrm{x} & \text { if } & \mathrm{x}<0\end{array}\right.\)

Also defined as \(\max \{\mathrm{x},-\mathrm{x}\}\)
Domain : R \(\quad\) Range \(:[0, \infty)\)

Note: \( f(x)=\dfrac{1}{|x|} \quad\) Domain : \(R-\{0\}\) Range : \(\mathrm{R}^{+}\)

Properties of modulus function:

For any \(\mathrm{x}, \mathrm{y}, \mathrm{a} \in \mathrm{R}\)

(i) \(|x| \geq 0\)     (ii) \(|x|=|-x|\)
(iii) \(|x y|=|x||y|\)      (iv) \(\left|\dfrac{\mathrm{x}}{\mathrm{y}}\right|=\dfrac{|\mathrm{x}|}{|\mathrm{y}|} ; \mathrm{y} \neq 0\)
(v) \(|x|=a \Rightarrow x=\pm\) a, \(a>0\)    (vi) \(\sqrt{x^{2}}=|x|\)
(vii) \(|x| \geq a \Rightarrow x \geq a\) or \(x \leq-a\). where a is positive.
(viii) \(|x| \leq a \Rightarrow x \in[-a, a]\). where a is positive
(ix) \(|x|>|y| \Rightarrow x^{2}>y^{2}\)
(x) \(|| x|-| y|| \leq|x+y| \leq|x|+|y|\)
Note that \((\mathrm{a})|\mathrm{x}|+|\mathrm{y}|=|\mathrm{x}+\mathrm{y}| \Rightarrow \mathrm{xy} \geq 0\)
                  (b) \(|x|+|y|=|x-y| \Rightarrow x y \leq 0\)

(f) Signum function :

Graph of signum Function

Signum function \(y=\operatorname{sgn}(x)\) is defined as follows

\(y=\left\{\begin{array}{l}\frac{|x|}{x}, x \neq 0 \\ 0, x=0\end{array}=\left\{\begin{array}{ll}1 & \text { for } x>0 \\ 0 & \text { for } x=0 \\ -1 & \text { for } x<0\end{array}\right.\right.\)

Domain: \(\mathrm{R}\)
Range: \(\{-1,0,1\}\)

(g) Greatest integer or step up function:

Graph of Greatest integer or step up function

The function \(y=f(x)=[x]\) is called the greatest integer function where \([\mathrm{x}]\) denotes the greatest integer less than or equal to \(x\). Note that for :

\(\begin{array}{|c|c|} \hline x & [x] \\ \hline [–2,–1)& –2 \\ \hline [–1,0)& –1 \\ \hline [0,1)& 0 \\ \hline [1,2)& 1 \\ \hline \end{array}\)

Domain : \(\mathrm{R}\)
Range : I

Properties of greatest integer function:

(i) \(x-1<[x] \leq x<[x]+1,0 \leq x-[x]<1\)

(ii) \([x+y]=\left\{\begin{array}{ll}{[x]+[y]}, & \{x\}+\{y\} \in[0,1) \\ {[x]+[y]+1,} & \{x\}+\{y\} \in[1,2)\end{array}\right.\)

(iii) \([x]+[-x]=\left\{\begin{array}{ll}0, & x \in I \\ -1, & x \notin I\end{array}\right.\)

(iv) \(\{x\}+\{-x\}=\left\{\begin{array}{ll}0, & x \in I \\ 1, & x \notin I\end{array}\right.\)


Note: \( f(x)=\frac{1}{[x]}\)

Domain : \(\mathrm{R}-[0,1) \quad\) Range : \(\left\{\mathrm{x} \mid \mathrm{x}=\frac{1}{\mathrm{n}}, \mathrm{n} \in \mathrm{I}-\{0\}\right\}\)

(h) Fractional part function:

It is defined as: \(g(x)=\{x\}=x-[x]\) e.g.

Graph of Fraction part Function

\(\begin{array}{|c|c|}\hline \mathrm{x} & \{\mathrm{x}\} \\\hline [-2,-1) & \mathrm{x}+2 \\\hline [-1,0) & \mathrm{x}+1 \\\hline [0,1) & \mathrm{x}\\\hline [1,2) & \mathrm{x}-1 \\\hline\end{array}\)

\(\begin{array}{lll}\mathbf{Domain :} \mathrm{R} & \mathbf { Range : }[0,1) & \mathbf{ Period : } 1\end{array}\)

Note: \( f(x)=\frac{1}{\{x\}} \quad\) Domain : \(R-I \quad\) Range: \((1, \infty)\)

(i) Identity function:

Graph of identity Function
The function \(\mathrm{f}: \mathrm{A} \rightarrow \mathrm{A}\) defined by \(\mathrm{f}(\mathrm{x})=\mathrm{x} \,\, \forall \,\, \mathrm{x} \in \mathrm{A}\) is called the identity function on A and is denoted by \(\mathrm{I}_{\mathrm{A}}\).

(j) Constant function:

Graph of constant function
\(\mathrm{f}: \mathrm{A} \rightarrow \mathrm{B}\) is said to be constant function if every element of \(A\) has the same f image in \(B\). Thus \(\mathrm{f}: \mathrm{A} \rightarrow \mathrm{B} ; \mathrm{f}(\mathrm{x})=\mathrm{c}, \forall \mathrm{x} \in \mathrm{A}\) \(\mathrm{c} \in \mathrm{B}\) is constant function.

Domain : \(\mathrm{R} \quad\) Range: \(\{\mathrm{c}\}\)

(k) Trigonometric functions:

(i) Sine function: \(\mathrm{f}(\mathrm{x})=\sin \mathrm{x}\)
Domain : \(\mathrm{R} \quad\) Range: \([-1,1]\), period \(2 \pi\)

(ii) Cosine function : \(f(x)=\cos x\)
Domain : R \(\quad\) Range: \([-1,1]\), period \(2 \pi\)

(iii) Tangent function : \(f(x)=\tan x\)
Domain : \(\mathrm{R}-\left\{\mathrm{x} \mid \mathrm{x}=\frac{(2 \mathrm{n}+1) \pi}{2}, \mathrm{n} \in \mathrm{I}\right\}\)
Range : \(\mathrm{R}\), period \(\pi\)

(iv) Cosecant function : \(f(x)=\operatorname{cosec} x\)
Domain : \(\mathrm{R}-\{\mathrm{x} \mid \mathrm{x}=\mathrm{n} \pi, \mathrm{n} \in \mathrm{I}\)
Range : \(\mathrm{R}-(-1,1)\), period \(2 \pi\)

(v) Secant function : \(\mathrm{f}(\mathrm{x})=\sec \mathrm{x}\)
Domain : \(\mathrm{R}-\{\mathrm{x} \mid \mathrm{x}=(2 \mathrm{n}+1) \pi / 2: \mathrm{n} \in \mathrm{I}\}\)
Range : \(\mathrm{R}-(-1,1)\), period \(2 \pi\)

(vi) Cotangent function : \(f(x)=\cot x\)
Domain : \(\mathrm{R}-\{\mathrm{x} \mid \mathrm{x}=\mathrm{n} \pi, \mathrm{n} \in \mathrm{I}\}\)
Range : R, period \(\pi\)

(l) Inverse Trigonometric function:

\(\scriptsize\mathbf{{\begin{array}{|c|c|c|c|} \hline (i) & \mathrm{f}(\mathrm{x})=\sin ^{-1} \mathrm{x}  & Domain :[-1,1] & Range :\left[-\frac{\pi}{2}, \frac{\pi}{2}\right] \\ \hline (ii) & f(x)=\cos ^{-1} x & Domain :[-1,1] & Range :[0, \pi]\\ \hline (iii) & f(x)=\tan ^{-1} x & Domain : R & Range :\left(-\frac{\pi}{2}, \frac{\pi}{2}\right) \\ \hline  (iv) &  f(x)=\cot ^{-1} x &  Domain :  R &  Range :(0, \pi)\\ \hline (v)& \mathrm{f}(\mathrm{x})=\operatorname{cosec}^{-1} \mathrm{x}  & Domain : \mathrm{R}-(-1,1)  & Range : \left[-\frac{\pi}{2}, \frac{\pi}{2}\right]-\{0\}\\ \hline (vi) & \mathrm{f}(\mathrm{x})=\sec ^{-1} \mathrm{x} & Domain : \mathrm{R}-(-1,1) & Range :[0, \pi]-\left\{\frac{\pi}{2}\right\} \\ \hline \end{array}}}\)


4. EQUAL OR IDENTICAL FUNCTION :

Two function \(\mathrm{f} \) & \( \mathrm{~g}\) are said to be equal if :

(a) The domain of \(\mathrm{f}=\) the domain of \(\mathrm{g}\)
(b) The range of \(\mathrm{f}=\) range of \(\mathrm{g}\) and
(c) \(\mathrm{f}(\mathrm{x})=\mathrm{g}(\mathrm{x})\), for every \(\mathrm{x}\) belonging to their common domain (i.e. should have the same graph)


5. ALGEBRAIC OPERATIONS ON FUNCTIONS :

If \(\mathrm{f} \) & \(\mathrm{~g}\) are real valued functions of \(\mathrm{x}\) with domain set \(\mathrm{A}, \mathrm{B}\) respectively, \(\mathrm{f}+\mathrm{g}, \mathrm{f}-\mathrm{g},(\mathrm{f} \cdot \mathrm{g}) \) & \((\mathrm{f} / \mathrm{g})\) as follows:

(a) \((f \pm g)(x)=f(x) \pm g(x)\), domain in each case is \(A \cap B\)
(b) \((f . g)(x)=f(x) \cdot g(x)\), domain is \(A \cap B\)
(c) \(\left(\dfrac{\mathrm{f}}{\mathrm{g}}\right)(\mathrm{x})=\dfrac{\mathrm{f}(\mathrm{x})}{\mathrm{g}(\mathrm{x})}\), domain \(\mathrm{A} \cap \mathrm{B}-\{\mathrm{x} \mid \mathrm{g}(\mathrm{x})=0\}\)


6. CLASSIFICATION OF FUNCTIONS :

(a) One-One function (Injective mapping):

A function \(\mathrm{f}: \mathrm{A} \rightarrow \mathrm{B}\) is said to be a one-one function or injective mapping if different elements of A have different \(f\) images in \(B\). Thus for \(x_{1}, x_{2} \in A \& f\left(x_{1}\right), f\left(x_{2}\right) \in B, f\left(x_{1}\right)=f\left(x_{2}\right)\)\(\Leftrightarrow \mathrm{x}_{1}=\mathrm{x}_{2}\) or \(\mathrm{x}_{1} \neq \mathrm{x}_{2} \Leftrightarrow \mathrm{f}\left(\mathrm{x}_{1}\right) \neq \mathrm{f}\left(\mathrm{x}_{2}\right)\)

Note:
(i) Any continuous function which is entirely increasing or decreasing in whole domain is one-one.
(ii) If a function is one-one, any line parallel to \(\mathrm{x}\) -axis cuts the graph of the function at atmost one point
(iii) Non-monotonic function can also be injective.

(b) Many-one function:

A function \(\mathrm{f}: \mathrm{A} \rightarrow \mathrm{B}\) is said to be a many one function if two or more elements of A have the same f image in B. Thus \(\mathrm{f}: \mathrm{A} \rightarrow \mathrm{B}\) is many one if \(\exists \mathrm{x}_{1}, \mathrm{x}_{2} \in \mathrm{A}, \mathrm{f}\left(\mathrm{x}_{1}\right)=\mathrm{f}\left(\mathrm{x}_{2}\right)\) but \(x_{1} \neq x_{2}\)

Note : If a continuous function has local maximum or local minimum, then \(\mathrm{f}(\mathrm{x})\) is many-one because atleast one line parallel to \(x\) -axis will intersect the graph of function atleast twice.

Total number of functions= number of one-one functions + number of many-one function

(c) Onto function (Surjective) :

If range \(=\) co-domain, then \(\mathrm{f}(\mathrm{x})\) is onto.

(d) Into function :

If \(f: A \rightarrow B\) is such that there exists atleast one element in co-domain which is not the image of any element in domain, then \(\mathrm{f}(\mathrm{x})\) is into.

Note :

(i) If ' \(\mathrm{f}\) ' is both injective & surjective, then it is called a Bijective mapping. The bijective functions are also named as invertible, non singular or biuniform functions.
(ii) If a set A contains \(\mathrm{n}\) distinct elements then the number of different functions defined from \(\mathrm{A} \rightarrow \mathrm{A}\) is \(\mathrm{n}^{\mathrm{n}} \&\) out of it \(\mathrm{n} !\) are one one and rest are many one.

(iii) If \(f: R \rightarrow R\) is a polynomial
(a) Of even degree, then it will neither be injective nor surjective.
(b) Of odd degree, then it will always be surjective, no general comment can be given on its injectivity.


7. COMPOSITE OF UNIFORMLY & NON-UNIFORMLY DEFINED FUNCTION :

Let \(\mathrm{f}: \mathrm{A} \rightarrow \mathrm{B} \) & \( \mathrm{~g}: \mathrm{B} \rightarrow \mathrm{C}\) be two functions. Then the function gof : \(\mathrm{A} \rightarrow \mathrm{C}\) defined by (gof ) \((\mathrm{x})=\mathrm{g}(\mathrm{f}(\mathrm{x})) \,\, \forall \,\, \mathrm{x} \in \mathrm{A}\) is called the composite of the two functions \(f \) & \(g\).

Hence in gof(x) the range of 'f' must be a subset of the domain of 'g'.
\( \text{x}\rightarrow \boxed{\mathrm{f}}\rightarrow \boxed{\mathrm{g}}\rightarrow  \mathrm{g(f(x))}\)

Properties of composite functions:

(a) In general composite of functions is not commutative i.e. gof \(\neq\) fog
(b) The composite of functions is associative i.e. if \(f, g, h\) are three functions such that fo(goh) & (fog)oh are defined, then \(\mathrm{fo}(\mathrm{goh})=(\) fog \() \mathrm{oh}\)
(c) The composite of two bijections is a bijection i.e. if \(f \) & \(g\) are two bijections such that gof is defined, then gof is also a bijection.
(d) If gof is one-one function then \(\mathrm{f}\) is one-one but \(g\) may not be one-one.


8. HOMOGENEOUS FUNCTIONS :

A function is said to be homogeneous with respect to any set of variables when each of its terms is of the same degree with respect to those variables.

For examples \(5 x^{2}+3 y^{2}-x y\) is homogenous in \(x \) & \(y\). Symbolically if, \(\mathrm{f}(\mathrm{tx}, \mathrm{ty})=\mathrm{t}^{\mathrm{n}} \mathrm{f}(\mathrm{x}, \mathrm{y})\), then \(\mathrm{f}(\mathrm{x}, \mathrm{y})\) is homogeneous function of degree \(\mathrm{n}\).


9. BOUNDED FUNCTION :

A function is said to be bounded if \(\mathrm{I} \mathrm{f}(\mathrm{x}) \mid \leq \mathrm{M}\), where \(\mathrm{M}\) is a finite quantity.


10. IMPLICIT & EXPLICIT FUNCTION :

A function defined by an equation not solved for the dependent variable is called an implicit function. e.g. the equation \(x^{3}+y^{3}=1\) defines \(y\) as an implicit function of \(x\). If \(y\) has been expressed in terms of \(x\) alone then it is called an Explicit function.


11. INVERSE OF A FUNCTION :

Let \(\mathrm{f}: \mathrm{A} \rightarrow \mathrm{B}\) be a one-one & onto function, then their exists a unique function \(g: B \rightarrow A\) such that \(f(x)=y \Leftrightarrow g(y)=x\) \(\forall \, x \in A \,\, \& \,\, y \in B\). Then \(g\) is said to be inverse of \(f\). Thus \(\left.g=\mathrm{f}^{-1}: \mathrm{B} \rightarrow \mathrm{A}=\{(\mathrm{f}(\mathrm{x}), \mathrm{x})) \mid(\mathrm{x}, \mathrm{f}(\mathrm{x})) \in \mathrm{f}\right\}\)

Properties of inverse function:

(a) The inverse of a bijection is unique.
(b) If \(\mathrm{f}: \mathrm{A} \rightarrow \mathrm{B}\) is a bijection & \( \mathrm{~g}: \mathrm{B} \rightarrow \mathrm{A}\) is the inverse of \(\mathrm{f}\), then fog \(=I_{B}\) and gof \(=I_{A}\), where \(I_{A} \) & \(I_{B}\) are identity functions on the sets \(A \) & \(B\) respectively. If fof \(=I\), then \(f\) is inverse of itself.
(c) The inverse of a bijection is also a bijection.
(d) If \(f \) & \( g\) are two bijections \(f: A \rightarrow B, g: B \rightarrow C \) & gof exist, then the inverse of gof also exists and \((\mathrm{gof})^{-1}=\mathrm{f}^{-1} \mathrm{og}^{-1}\).
(e) Since \(f(a)=b\) if and only if \(f^{-1}(b)=a\), the point \((a, b)\) is on the graph of 'f' if and only if the point \((b, a)\) is on the graph of \(f^{-1}\). But we get the point \((b, a)\) from \((a, b)\) by reflecting about the line \(y=x\). In general \(\mathrm{f}(\mathrm{x})=\mathrm{x} \Rightarrow \mathrm{f}(\mathrm{x})=\mathrm{f}^{-1}(\mathrm{x})\).
How to make inverse graph

The graph of \(\mathbf{f}^{-1}\) is obtained by reflecting the graph of \(\mathbf{f}\) about the line \(\mathbf{y}=\mathbf{x}\).


12. ODD & EVEN FUNCTIONS :

If a function is such that whenever 'x' is in it's domain '-x' is also in it's domain & it satisfies 
\(\mathrm{f}(-\mathrm{x})=\mathrm{f}(\mathrm{x})\), then it is an even function and if
\(\mathrm{f}(-\mathrm{x})=-\mathrm{f}(\mathrm{x})\), then it is an odd function

Note :
(i) A function may neither be odd nor even.
(ii) Inverse of an even function is not defined, as it is many-one function.
(iii) Every even function is symmetric about the y-axis & every odd function is symmetric about the origin.
(iv) Every function which has '-x' in it's domain whenever 'x' is in it's domain, can be expressed as the sum of an even & an odd function.
e.g. \(f(x)=\underbrace{\dfrac{f(x)+f(-x)}{2}}_{\text{Even}}+\underbrace{\dfrac{f(x)-f(-x)}{2}}_{\text{Odd}} \)
(v) The only function which is defined on the entire number line & even and odd at the same time is \(f(x)=0\).
(vi) If \(\mathrm{f}(\mathrm{x})\) and \(g(\mathrm{x})\) both are even or both are odd then the function \(\mathrm{f}(\mathrm{x}) \cdot \mathrm{g}(\mathrm{x})\). will be even but if any one of them is odd & other is even, then \(\mathrm{f} . \mathrm{g}\) will be odd.


13. PERIODIC FUNCTION :

A function f(x) is called periodic if there exists a positive number T(T >0) called the period of the function such that f(x + T) = f(x) = f(x – T), for all values of x within the domain of f(x) and least positive T if exist called fundamental period.
Note :
(i) Inverse of a periodic function does not exist.
(ii) Every constant function is periodic, with no fundamental period.
(iii) If f(x) has a period T & g(x) also has a period T then it does not mean that f(x) + g(x) must have a period T. e.g. f(x) = |sin x|+|cos x| (here period means fundamental period).
(iv) If f(x) has period p and g(x) has period q, then one of the period of f(x) + g(x) will be LCM of p & q. However it may not be fundamental period.
(v) If f(x) has period p, then \(\dfrac{1}{f(x)}\) and \(\sqrt{f(x)}\) (provided each one is defined over some non empty set) also has a period p.
(vi) If f(x) has period T then f(ax + b) has a period T/a (a > 0).
(vii) |sinx|, |cosx|, |tanx|, |cotx|, |secx| &  |cosecx| are periodic function with period p.
(viii) sin\(^n\)x, cos\(^n\)x, sec\(^n\)x, cosec\(^n\)x, are periodic function with period 2π when ‘n’ is odd or π when n is even.
(ix) tan\(^n\)x, cos\(^n\)x are periodic function with period π.


14. GENERAL :

If x, y are independent variables and f is continuous function, then :
(a) f(xy) = f(x) + f(y) \(\Rightarrow\) f(x) = k.ln x
(b) f(xy) = f(x) . f(y) \(\Rightarrow\) f(x) = \(x^n\), n \(\in\) R or f(x) = 0.
(c) f(x + y) = f(x) . f(y) \(\Rightarrow\) f(x) = \(a^{kx}\) or f(x) = 0.
(d) f(x + y) = f(x) + f(y) \(\Rightarrow\) f(x) = kx, where k is a constant.


15. SOME BASIC FUNCTION & THEIR GRAPH:

(a) 

Graph of x², x⁴
y = \(x^{2n}\), where n \(\in\) N

(b) 

Graph of x³, x⁵
y = \(x^{2n+1}\), where n \(\in\) N

(c)

Graph of 1/x , 1/x³

 y = \(\dfrac{1}{x^{2n-1}}\), where n \(\in\) N

(d)

Graph of 1/x², 1/x⁴
y = \(\dfrac{1}{x^{2n}}\), where n \(\in\) N

(e)

Graph of √x, x^(1/4)
y = \(x^{\frac{1}{x^{2n}}}\), where n \(\in\) N

(f)

Graph of x^(1/3), x^(1/5)
y =  \(x^{\frac{1}{x^{2n+1}}}\), where n \(\in\) N

Note:

Graph of x^(2/3)
 y = \(x^{\frac{2}{3}}\)

(g) y = \(\log_ax\)

Graph of ln x or logx

(h) y = \(a^x\)

Graph of a^x, e^x

(i) Trigonometric functions :

y = sinx

Trigonometry function graph of sinx

y = cosx

Trigonometry function graph of cosx

y = tanx

Trigonometry function graph of tanx

y = cosecx
Trigonometry function graph of cosecx

y = secx

Trigonometry function graph of secx

y = cotx

Trigonometry function graph of cotx

(j) y = ax\(^2\)+ bx + c
vertex \(\left(-\dfrac{b}{2a},-\dfrac{D}{4a}\right)\)
where D = b\(^2\)– 4ac
Quadratic discriminant


16. TRANSFORMATION OF GRAPH :

(a) when ƒ(x) transforms to ƒ(x) + k
if k > 0 then shift graph of ƒ(x) upward through k
if k < 0 then shift graph of ƒ(x) downward through k
Examples :
when ƒ(x) transforms to ƒ(x) + k

(b) ƒ(x) transforms to ƒ(x + k) :
if k > 0 then shift graph of ƒ(x) through k towards left.
if k < 0 then shift graph of ƒ(x) through k towards right.
Examples : 
ƒ(x) transforms to ƒ(x + k)

(c) ƒ (x) transforms to kƒ(x) :
if k > 1 then stretch graph of ƒ(x) k times along y-axis
if 0 < k < 1 then shrink graph of ƒ(x), k times along y-axis
Examples : 
ƒ (x) transforms to kƒ(x)

(d) ƒ(x) transforms to ƒ(kx) :
if k > 1 then shrink graph of ƒ (x), ‘k’ times along x-axis
if 0 < k < 1 then stretch graph of ƒ(x), ‘k’ times along x-axis
Examples :
ƒ(x) transforms to ƒ(kx)

(e) ƒ(x) transforms to ƒ(–x) :
Take mirror image of the curve y = ƒ(x) in y-axis as plane mirror
Example :
ƒ(x) transforms to ƒ(–x)
(f) ƒ(x) transforms to –ƒ(x) :
Take image of y = ƒ(x) in the x axis as plane mirror
Example :
ƒ(x) transforms to –ƒ(x)

(g) ƒ(x) transforms to |ƒ (x)| :
Take mirror image (in a axis) of the portion of the graph of
ƒ(x) which lies below x-axis.
Examples :
ƒ(x) transforms to |ƒ (x)|

(h) ƒ(x) transforms to ƒ(|x|) :
Neglect the curve for x < 0 and take the image of curve for
x ≥ 0 about y-axis.
ƒ(x) transforms to ƒ(|x|)

(i) y = ƒ(x) transforms to |y|= ƒ(x) :
Remove the portion of graph which lies below x-axis & then
take mirror image {in x axis} of remaining portion of graph
Examples :
y = ƒ(x) transforms to |y|= ƒ(x)


Labels:

Comments

Post a Comment

Popular posts from this blog

Indefinite Integration - Notes, Concept and All Important Formula

INDEFINITE INTEGRATION If  f & F are function of \(x\) such that \(F^{\prime}(x)\) \(=f(x)\) then the function \(F\) is called a PRIMITIVE OR ANTIDERIVATIVE OR INTEGRAL of \(\mathrm{f}(\mathrm{x})\) w.r.t. \(\mathrm{x}\) and is written symbolically as \(\displaystyle \int \mathrm{f}(\mathrm{x}) \mathrm{d} \mathrm{x}\) \(=\mathrm{F}(\mathrm{x})+\mathrm{c} \Leftrightarrow \dfrac{\mathrm{d}}{\mathrm{dx}}\{\mathrm{F}(\mathrm{x})+\mathrm{c}\}\) \(=\mathrm{f}(\mathrm{x})\) , where \(\mathrm{c}\) is called the constant of integration. Note : If \(\displaystyle \int f(x) d x\) \(=F(x)+c\) , then \(\displaystyle \int f(a x+b) d x\) \(=\dfrac{F(a x+b)}{a}+c, a \neq 0\) All Chapter Notes, Concept and Important Formula 1. STANDARD RESULTS : (i) \( \displaystyle \int(a x+b)^{n} d x\) \(=\dfrac{(a x+b)^{n+1}}{a(n+1)}+c ; n \neq-1\) (ii) \(\displaystyle \int \dfrac{d x}{a x+b}\) \(=\dfrac{1}{a} \ln|a x+b|+c\) (iii) \(\displaystyle \int e^{\mathrm{ax}+b} \mathrm{dx}\) \(=\dfrac{1}{...
Post a Comment
Read more

Logarithm - Notes, Concept and All Important Formula

LOGARITHM LOGARITHM OF A NUMBER : The logarithm of the number \(\mathrm{N}\) to the base ' \(\mathrm{a}\) ' is the exponent indicating the power to which the base 'a' must be raised to obtain the number \(\mathrm{N}\) . This number is designated as \(\log _{\mathrm{a}} \mathrm{N}\) . (a) \(\log _{a} \mathrm{~N}=\mathrm{x}\) , read as \(\log\) of \(\mathrm{N}\) to the base \(\mathrm{a} \Leftrightarrow \mathrm{a}^{\mathrm{x}}=\mathrm{N}\) . If \(a=10\) then we write \(\log N\) or \(\log _{10} \mathrm{~N}\) and if \(\mathrm{a}=e\) we write \(\ln N\) or \(\log _{e} \mathrm{~N}\) (Natural log) (b) Necessary conditions : \(\mathrm{N}> \,\,0 ; \,\, \mathrm{a}> \,\,0 ; \,\, \mathrm{a} \neq 1\) (c) \(\log _{a} 1=0\) (d) \(\log _{a} a=1\) (e) \(\log _{1 / a} a=-1\) (f) \(\log _{a}(x . y)=\log _{a} x+\log _{a} y ; \,\, x, y> \,\,0\) (g) \(\log _{a}\left(\dfrac{\mathrm{x}}{y}\right)=\log _{\mathrm{a}} \mathrm{x}-\log _{\mathrm{a}} \mathrm{y} ; \,\, \mathrm{...
Post a Comment
Read more

Hyperbola - Notes, Concept and All Important Formula

HYPERBOLA The Hyperbola is a conic whose eccentricity is greater than unity \((e>1) .\) 1. STANDARD EQUATION & DEFINITION(S): Standard equation of the hyperbola is \(\dfrac{\mathbf{x}^{2}}{\mathbf{a}^{2}}-\dfrac{\mathbf{y}^{2}}{\mathbf{b}^{2}}=\mathbf{1},\) where \(b^{2}=a^{2}\left(e^{2}-1\right)\) or \(a^{2} e^{2}=a^{2}+b^{2}\)    i.e.    \(e^{2}=1+\dfrac{b^{2}}{a^{2}}\) \(=1+\left(\dfrac{\text { Conjugate Axis }}{\text { Transverse Axis }}\right)^{2}\) (a) Foci : \(\mathrm{S} \equiv(\mathrm{a} e, 0) \quad \& \quad \mathrm{~S}^{\prime} \equiv(-\mathrm{a} e, 0) .\) (b) Equations of directrices: \(\mathrm{x}=\dfrac{\mathrm{a}}{e}\quad \) & \(\quad \mathrm{x}=-\dfrac{\mathrm{a}}{e}\) (c) Vertices: \(A \equiv(a, 0)\quad \) & \(\quad A^{\prime} \equiv(-a, 0)\) (d) Latus rectum: (i) Equation: \(\mathrm{x}=\pm \mathrm{ae}\) (ii) Length:  \(\begin{aligned} &=\dfrac{2 b^{2}}{a}=\dfrac{(\text { Conjugate Axis })^{2}}{(\text { Transverse Axis ...
Post a Comment
Read more