Circle- Notes, Concept and All Important Formula

CIRCLE

1. DEFINITION :

A circle is the locus of a point which moves in a plane in such a way that its distance from a fixed point remains constant. The fixed point is called the centre of the circle and the constant distance is called the radius of the circle.

---

All Chapter Notes, Concept and Important Formula

---

2. STANDARD EQUATIONS OF THE CIRCLE :

(a) Central Form:

If $(\mathrm{h}, \mathrm{k})$ is the centre and $\mathrm{r}$ is the radius of the circle then its equation is $(\mathbf{x}-\mathbf{h})^{2}+(\mathbf{y}-\mathbf{k})^{2}=\mathbf{r}^{2}$

(b) General equation of circle :

$\mathbf{x}^{2}+\mathbf{y}^{2}+\mathbf{2 g x}+\mathbf{2 f y}+\mathbf{c}=\mathbf{0}$, where $g, \mathrm{f}, c$ are constants and centre is $(-g,-f)$

i.e. $\left(-\frac{\text { coefficient of } \mathrm{x}}{2},-\frac{\text { coefficient of } \mathrm{y}}{2}\right)$ and radius $r=\sqrt{g^{2}+f^{2}-c}$

Note : The general quadratic equation in $\mathrm{x}$ and $\mathrm{y}$, $a x^{2}+b y^{2}+2 h x y+2 g x+2 f y+c=0$ represents a circle if :

(i) coefficient of $x^{2}=$ coefficient of $y^{2}$ or $a=b \neq 0$
(ii) coefficient of $x y=0$ or $h=0$
(iii) $\left(g^{2}+f^{2}-c\right) \geq 0$ (for a real circle)

(c) Intercepts cut by the circle on axes:

The intercepts cut by the circle $x^{2}+y^{2}+2 g x+2 f y+c=0$ on:

(i) $x$ -axis $=2 \sqrt{g^{2}-c}$
(ii) $y$ -axis $=2 \sqrt{f^{2}-c}$

Note :

Intercept cut by a line on the circle $x^{2}+y^{2}+2 g x+2 f y+c=0$ or length of chord of the circle $=2 \sqrt{a^{2}-p^{2}}$ where a is the radius and $\mathrm{P}$ is the length of perpendicular from the centre to the chord.

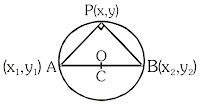
(d) Diameter form of circle :

If $\mathrm{A}\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right)$ and $\mathrm{B}\left(\mathrm{x}_{2}, \mathrm{y}_{2}\right)$ are the end points of the diameter of the circle then the equation of the circle is given by $\left(x-x_{1}\right)\left(x-x_{2}\right)+\left(y-y_{1}\right)\left(y-y_{2}\right)=0$

(e) The parametric forms of the circle:

(i) The parametric equation of the circle $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{r}^{2}$ are $\mathbf{x}=\mathbf{r} \cos \theta, \mathbf{y}=\mathbf{r} \sin \theta ; \theta \in[0,2 \pi)$

(ii) The parametric equation of the circle $(x-h)^{2}+(y-k)^{2}=r^{2}$ is $\mathbf{x}=\mathbf{h}+\mathbf{r} \cos \theta, \mathbf{y}=\mathbf{k}+\mathbf{r} \sin \theta$ where $\theta$ is parameter.

(iii) The parametric equation of the circle $x^{2}+y^{2}+2 g x+2 f y+c=0$ are $x=-g+\sqrt{g^{2}+f^{2}-c} \cos \theta,$ $y=-f+\sqrt{g^{2}+f^{2}-c} \sin \theta$ where $\theta$ is parameter.

Note that equation of a straight line joining two point $\alpha$ & $\beta$ on the circle $x^{2}+y^{2}=a^{2}$ is $x \cos \frac{\alpha+\beta}{2}+y \sin \frac{\alpha+\beta}{2}=a \cos \frac{\alpha-\beta}{2}$

---

---

3. POSITION OF A POINT W.R.T CIRCLE :

(a) Let the circle is $\mathrm{x}^{2}+y^{2}+2 \mathrm{gx}+2 \mathrm{fy}+\mathrm{c}=0$ and the point is $\left(x_{1}, y_{1}\right)$ then :
Point $\left(x_{1}, y_{1}\right)$ lies out side the circle or on the circle or inside the circle according as
$\Rightarrow \mathrm{S}_{1}=\mathrm{x}_{1}^{2}+y_{1}^{2}+2 \mathrm{gx}_{1}+2 \mathrm{fy}_{1}+\mathrm{c}>$ or $=$ or $<0$

(b) The greatest $\&$ the least distance of a point $A$ from a circle with centre $C$ & radius $r$ is $A C+r$ & $|A C-r|$ respectively.

(c) The power of point is given by $\mathrm{S}_{1}$.

---

---

4. TANGENT LINE OF CIRCLE :

When a straight line meet a circle on two coincident points then it is called the tangent of the circle.

(a) Condition of Tangency:

The line $L=0$ touches the circle $\mathrm{S}=0$ if $\mathrm{P}$ the length of the perpendicular from the centre to that line and radius of the circle $\mathrm{r}$ are equal i.e. $\mathrm{P}=\mathrm{r}$

(b) Equation of the tangent $(\mathbf{T}=\mathbf{0})$ :

(i) Tangent at the point $\left(x_{1}, y_{1}\right)$ on the circle $x^{2}+y^{2}=a^{2}$ is $\mathbf{x x}_{1}+\mathbf{y y}_{1}=\mathbf{a}^{2}$

(ii) (1) The tangent at the point (acost, asin t) on the circle $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{a}^{2}$ is $\mathbf{x c o s} \mathbf{t}+\mathbf{y} \sin \mathbf{t}=\mathbf{a}$
      (2) The point of intersection of the tangents at the points $\mathrm{P}(\alpha)$ and $\mathrm{Q}(\beta)$ is $\left(\frac{\mathrm{a} \cos \frac{\alpha+\beta}{2}}{\cos \frac{\alpha-\beta}{2}}, \frac{\mathrm{a} \sin \frac{\alpha+\beta}{2}}{\cos \frac{\alpha-\beta}{2}}\right) .$

(iii) The equation of tangent at the point $\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right)$ on the circle $x^{2}+y^{2}+2 g x+2 f y+c=0$ is
$\mathrm{xx}_{1}+\mathrm{yy}_{1}+\mathrm{g}\left(\mathrm{x}+\mathrm{x}_{1}\right)+\mathrm{f}\left(\mathrm{y}+\mathrm{y}_{1}\right)+\mathrm{c}=\mathbf{0}$

(iv) If line $y=m x+c$ is a straight line touching the circle $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{a}^{2}$, then $\mathrm{c}=\pm \mathrm{a} \sqrt{1+\mathrm{m}^{2}}$ and contact points are $\left(\mp \frac{\mathrm{am}}{\sqrt{1+\mathrm{m}^{2}}}, \pm \frac{\mathrm{a}}{\sqrt{1+\mathrm{m}^{2}}}\right)$ or $\left(\mp \frac{\mathrm{a}^{2} \mathrm{~m}}{\mathrm{c}}, \pm \frac{\mathrm{a}^{2}}{\mathrm{c}}\right)$ and equation of tangent is $y=m x \pm a \sqrt{1+m^{2}}$

(v) The equation of tangent with slope $\mathrm{m}$ of the circle $(x-h)^{2}+(y-k)^{2}=a^{2}$ is $(y-k)=m(x-h) \pm a \sqrt{1+m^{2}}$

Note:

To get the equation of tangent at the point $\left(\mathrm{x}_{1} \mathrm{y}_{1}\right)$ on any curve we replace $\mathrm{xx}_{1}$ in place of $\mathrm{x}^{2}, \mathrm{y} \mathrm{y}_{1}$ in place of $\mathrm{y}^{2}, \frac{\mathrm{x}+\mathrm{x}_{1}}{2}$ in place of $\mathrm{x}, \frac{\mathrm{y}+\mathrm{y}_{1}}{2}$ in place of $\mathrm{y}, \frac{\mathrm{x} \mathrm{y}_{1}+\mathrm{yx}_{1}}{2}$ in place of $\mathrm{xy}$ and $\mathrm{c}$ in place of c.

(c) Length of tangent $\left(\sqrt{\mathbf{S}_{1}}\right)$ :

The length of tangent drawn from point $\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right)$ out side the circle

$\mathrm{S} \equiv \mathrm{x}^{2}+\mathrm{y}^{2}+2 \mathrm{gx}+2 \mathrm{fy}+\mathrm{c}=0 \mathrm{is}$
$\mathrm{PT}=\sqrt{\mathrm{S}_{1}}=\sqrt{\mathrm{x}_{1}^{2}+\mathrm{y}_{1}^{2}+2 \mathrm{gx}_{1}+2 \mathrm{fy}_{1}+\mathrm{c}}$

(d) Equation of Pair of tangents $\left(\mathbf{S S}_{1}=\mathbf{T}^{2}\right)$ :

Let the equation of circle $S \equiv x^{2}+y^{2}=a^{2}$ and $P\left(x_{1}, y_{1}\right)$ is any point outside the circle. From the pointwe can draw two real and distinct tangent PQ & PR and combine equation of pair of tangents is -

$\left(x^{2}+y^{2}-a^{2}\right)\left(x_{1}^{2}+y_{1}^{2}-a^{2}\right)=\left(x x_{1}+y y_{1}-a^{2}\right)^{2}$ or $S S_{1}=T^{2}$

---

---

5. NORMAL OF CIRCLE :

Normal at a point of the circle is the straight line which is perpendicular to the tangent at the point of contact and passes through the centre of circle.

(a) Equation of normal at point $\left(x_{1}, y_{1}\right)$ of circle $x^{2}+y^{2}+2 g x+2 f y+c=0$ is
$\mathbf{y}-\mathbf{y}_{1}=\left(\frac{\mathbf{y}_{1}+\mathbf{f}}{\mathbf{x}_{1}+\mathbf{g}}\right)\left(\mathbf{x}-\mathbf{x}_{1}\right)$

(b) The equation of normal on any point $\left(\mathrm{x}_{1}, y_{1}\right)$ of circle $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{a}^{2}$ is $\mathbf{\left(\frac{y}{x}=\frac{y_{1}}{x_{1}}\right)}$

---

---

6. CHORD OF CONTACT :

If two tangents $\mathrm{PT}_{1}$ & $\mathrm{PT}_{2}$ are drawn from the point $\mathrm{P}\left(\mathrm{x}_{1}\right.$, $y_{1}$ ) to the circle $\mathrm{S} \equiv \mathrm{x}^{2}+\mathrm{y}^{2}+2 \mathrm{gx}+2 \mathrm{fy}+\mathrm{c}=0$ then the equation of the chord of contact $\mathrm{T}_{1} \mathrm{~T}_{2}$ is: $\mathbf{\mathrm{xx}_{1}+\mathrm{y} \mathrm{y}_{1}+\mathrm{g}\left(\mathrm{x}+\mathrm{x}_{1}\right)+\mathrm{f}\left(\mathrm{y}+\mathrm{y}_{1}\right)+\mathrm{c}=0}$ (i.e. $\mathrm{T}=0$ same as equation of tangent).

---

---

7. EQUATIONOF THE CHORD WITHA GIVEN MIDDLE POINT $\left(\mathbf{T}=\mathbf{S}_{1}\right):$

The equation of the chord of the circle $S \equiv x^{2}+y^{2}+2 g x+2 f y+c=0$ in terms of its mid point $M\left(x_{1}, y_{1}\right)$ is $\mathbf{y}-\mathbf{y}_{1}=-\frac{\mathbf{x}_{1}+\mathbf{g}}{\mathbf{y}_{1}+\mathbf{f}}\left(\mathbf{x}-\mathbf{x}_{1}\right)$

This on simplification can be put in the form $\mathrm{xx}_{1}+y y_{1}+g\left(\mathrm{x}+\mathrm{x}_{1}\right)+\mathrm{f}\left(\mathrm{y}+\mathrm{y}_{1}\right)+\mathrm{c}$$=\mathrm{x}_{1}^{2}+\mathrm{y}_{1}^{2}+2 \mathrm{gx}_{1}+2 \mathrm{fy}_{1}+\mathrm{c}$ which is designated by $\mathbf{T}=\mathbf{S}_{\mathbf{1}}$.

---

---

8. DIRECTOR CIRCLE :

The locus of point of intersection of two perpendicular tangents to a circle is called director circle. Let the circle be $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{a}^{2}$, then the equation of director circle is $x^{2}+y^{2}=2 a^{2}$.
$\therefore$ director circle is a concentric circle whose radius is $\sqrt{2}$ times the radius of the circle.

Note :
The director circle of
$x^{2}+y^{2}+2 g x+2 f y+c=0$ is $x^{2}+y^{2}+2 g x+2 f y+2 c-g^{2}-f^{2}=0$

---

---

9. POLE AND POLAR :

Let any straight line through the given point $\mathrm{A}\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right)$ intersect the given circle $\mathrm{S}=0$ in two points $\mathrm{P}$ and $\mathrm{Q}$ and if the tangent of the circle at $P$ and $Q$ meet at the point $R$ then locus of point $\mathrm{R}$ is called polar of the point $\mathrm{A}$ and point $\mathrm{A}$ is called the pole, with respect to the given circle.

The equation of the polar is the $\mathrm{T}=0$, so the polar of point $\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right)$ w.r.t circle $x^{2}+y^{2}+2 g x+2 f y+c=0$ is $x x_{1}+y y_{1}+g\left(x+x_{1}\right)+f\left(y+y_{1}\right)+c=0$

Pole of a given line with respect to a circle
To find the pole of a line we assume the coordinates of the pole then from these coordinates we find the polar. This polar and given line represent the same line. Then by comparing the coefficients of similar terms we can get the coordinates of the pole. The pole of $\ell x+m y+n=0$
w.r.t. circle $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{a}^{2}$ will be $\left(\frac{-\ell \mathrm{a}^{2}}{\mathrm{n}}, \frac{-\mathrm{ma}^{2}}{\mathrm{n}}\right)$

---

---

10. FAMILY OF CIRCLES:

(a) The equation of the family of circles passing through the points of intersection of two circles $\mathrm{S}_{1}=0$ & $\mathrm{~S}_{2}=0$ is:
$\mathrm{S}_{1}+\mathrm{K} \mathrm{S}_{2}=0 \quad(\mathrm{~K} \neq-1)$

(b) The equation of the family of circles passing through the point of intersection of a circle $\mathrm{S}=0$ & a line $\mathrm{L}=0$ is given by $\mathrm{S}+\mathrm{KL}=0$.

(c) The equation of a family of circles passing through two given points $\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right) \&\left(\mathrm{x}_{2}, \mathrm{y}_{2}\right)$ can be written in the form :
$\left(x-x_{1}\right)\left(x-x_{2}\right)+\left(y-y_{1}\right)\left(y-y_{2}\right)$$+K\left|\begin{array}{lll}x & y & 1 \\ x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1\end{array}\right|=0$ where $K$ is parameter.

(d) The equation of a family of circles touching a fixed line $y-y_{1}=m\left(x-x_{1}\right)$ at the fixed point $\left(x_{1}, y_{1}\right)$ is $\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}$$+\mathrm{K}\left[\mathrm{y}-\mathrm{y}_{1}-\mathrm{m}\left(\mathrm{x}-\mathrm{x}_{1}\right)\right]=0$, where $\mathrm{K}$ is a parameter.

(e) Family of circles circumscribing a triangle whose sides are given by $\mathrm{L}_{1}=0 ; \mathrm{L}_{2}=0$ & $\mathrm{~L}_{3}=0$ is given by $; \mathrm{L}_{1} \mathrm{~L}_{2}+\lambda \mathrm{L}_{2} \mathrm{~L}_{3}+\mu \mathrm{L}_{3} \mathrm{~L}_{1}=0$ provided coefficient of $x y=0$  & coefficient of $x^{2}=$ coefficient of $y^{2}$.

(f) Equation of circle circumscribing a quadrilateral whose side in order are represented by the lines $\mathrm{L}_{1}=0, \mathrm{~L}_{2}=0, \mathrm{~L}_{3}=0$ $\&$ $\mathrm{L}_{4}=0$ are $\mathrm{L}_{1} \mathrm{~L}_{3}+\lambda \mathrm{L}_{2} \mathrm{~L}_{4}=0$ provided coefficient of $x^{2}=$ coefficient of $y^{2}$ and coefficient of $x y=0$.

---

---

11. DIRECT AND TRANSVERSE COMMON TANGENTS :

Let two circles having centre $\mathrm{C}_{1}$ and $\mathrm{C}_{2}$ and radii, $\mathrm{r}_{1}$ and $\mathrm{r}_{2}$ and $\mathrm{C}_{1} \mathrm{C}_{2}$ is the distance between their centres then :

(a) Both circles will touch :

(i) Externally if $C_{1} C_{2}=r_{1}+$ $\mathrm{r}_{2}$, point $\mathrm{P}$ divides $\mathrm{C}_{1} \mathrm{C}_{2}$ in the ratio $\mathrm{r}_{1}: \mathrm{r}_{2}$ (internally). In this case there are three common tangents.

(ii) Internally if $C_{1} C_{2}=\left|r_{1}-r_{2}\right|$, point $P$ divides $\mathrm{C}_{1} \mathrm{C}_{2}$ in the ratio $\mathrm{r}_{1}: \mathrm{r}_{2}$ externally and in this case there will be only one common tangent.

(b) The circles will intersect : 

when $\left|r_{1}-r_{2}\right|<C_{1} C_{2}<r_{1}$ $+\mathrm{r}_{2}$ in this case there are two common tangents.

(c) The circles will not intersect :

(i) One circle will lie inside the other circle if $\mathrm{C}_{1} \mathrm{C}_{2}<\left|\mathrm{r}_{1}-\mathrm{r}_{2}\right|$ In this case there will be no common tangent.

(ii) When circle are apart from each other then $\mathrm{C}_{1} \mathrm{C}_{2}>\mathrm{r}_{1}+\mathrm{r}_{2}$ and in this case there will be four common tangents. Lines $\mathrm{PQ}$ and $\mathrm{RS}$ are called transverse or indirect or internal common tangents and these lines meet line $\mathrm{C}_{1} \mathrm{C}_{2}$ on $\mathrm{T}_{1}$ and $\mathrm{T}_{1}$ divides the line $\mathrm{C}_{1} \mathrm{C}_{2}$ in the ratio $\mathrm{r}_{1}: \mathrm{r}_{2}$ internally and lines $A B \& C D$ are called direct or external common tangents. These lines meet $\mathrm{C}_{1} \mathrm{C}_{2}$ produced on $\mathrm{T}_{2}$. Thus $\mathrm{T}_{2}$ divides $\mathrm{C}_{1} \mathrm{C}_{2}$ externally in the ratio $\mathrm{r}_{1}: \mathrm{r}_{2}$.

Note : Length of direct common tangent $=\sqrt{\left(\mathrm{C}_{1} \mathrm{C}_{2}\right)^{2}-\left(\mathrm{r}_{1}-\mathrm{r}_{2}\right)^{2}}$
Length of transverse common tangent $=\sqrt{\left(\mathrm{C}_{1} \mathrm{C}_{2}\right)^{2}-\left(\mathrm{r}_{1}+\mathrm{r}_{2}\right)^{2}}$

---

---

12. THE ANGLE OF INTERSECTION OF TWO CIRCLES :

Definition : The angle between the tangents of two circles at the point of intersection of the two circles is called angle of intersection of two circles.

then $\cos \theta=\frac{2 g_{1} g_{2}+2 f_{1} f_{2}-c_{1}-c_{2}}{2 \sqrt{g_{1}^{2}+f_{1}^{2}-c_{1}} \sqrt{g_{2}^{2}+f_{2}^{2}-c_{2}}}$ or $\boxed{\cos \theta=\left(\frac{r_{1}^{2}+r_{2}^{2}-d^{2}}{2 r_{1} r_{2}}\right)}$

Here $\mathrm{r}_{1}$ and $\mathrm{r}_{2}$ are the radii of the circles and $\mathrm{d}$ is the distance between their centres.
If the angle of intersection of the two circles is a right angle then such circles are called "Orthogonal circles" and conditions for the circles to be orthogonal is $\mathbf{2 g_{1} g_{2}+2 f_{1} f_{2}=c_{1}+c_{2}}$

---

---

13. RADICAL AXIS OF THE TWO CIRCLES $\left(\mathbf{S}_{1}-\mathbf{S}_{2}=\mathbf{0}\right)$ :

Definition: The locus of a point, which moves in such a way that the length of tangents drawn from it to the circles are equal is called the radical axis. If two circles are

$\begin{array}{l}\mathrm{S}_{1} \equiv \mathrm{x}^{2}+\mathrm{y}^{2}+2 \mathrm{~g}_{1} \mathrm{x}+2 \mathrm{f}_{1} \mathrm{y}+\mathrm{c}_{1}=0 \\\mathrm{S}_{2} \equiv \mathrm{x}^{2}+\mathrm{y}^{2}+2 \mathrm{~g}_{2} \mathrm{x}+2 \mathrm{f}_{2} \mathrm{y}+\mathrm{c}_{2}=0\end{array}$

Then the equation of radical axis is given by $\mathbf{S}_{\mathbf{1}}-\mathbf{S}_{\mathbf{2}}=\mathbf{0}$

Note:
(i) If two circles touches each other then common tangent is radical axis.

(ii) If two circles cuts each other then common chord is radical axis.

(iii) If two circles cuts third circle orthogonally then radical axis of first two is locus of centre of third circle.
(iv) The radical axis of the two circles is perpendicular to the line joining the centre of two circles but not always pass through mid point of it.

---

---

14. Radical centre :

The radical centre of three circles is the point from which length of tangents on three circles are equal i.e. the point of intersection of radical axis of the circles is the radical centre of the circles.

Note:
(i) The circle with centre as radical centre and radius equal to the length of tangent from radical centre to any of the circle, will cut the three circles orthogonally.
(ii) If three circles are drawn on three sides of a triangle taking them as diameter then its orthocenter will be its radical centre.

---

---